5. Potential Flow¶
This tutorial demonstrates VisIt’s features while exploring results from simple simulations of potential based flow around an obstruction, specifically an airfoil. Potential flow assumes irrotational flow. That is, there is no rotational motion in the flow, no vortices or eddies. This assumption is valid for low velocities and certain types of gases/fluids and obstructions. When the flow does involve rotation, a more complex solution involving Navier-Stokes equations is required.
The potential flow solver is a mini-app developed using the MFEM finite element library. The example is available for this tutorial thanks to Aaron Fischer and Mark Miller of LLNL. The data set includes VTK output files for a set of solutions where the angle of attack of the velocity varies from -5 degrees to 25 degrees.
5.1. Open the dataset¶
This tutorial uses the potential flow dataset.
Download the potential flow dataset.
Click on the Open icon to bring up the File open window.
Navigate your file system to the folder containing “potential_flow_ang_sweep.visit”.
Highlight the file “potential_flow_ang_sweep.visit” and then click OK.
5.2. Plotting the mesh topology¶
First we will examine the mesh used by the solver.
5.2.1. Create a Mesh plot¶
Go to Add->Mesh->main.
Click Draw.
After this, the mesh plot is rendered in VisIt’s Viewer window. This is a 2D mesh, modify the view by planning and zooming in the viewer window. Zoom in near the airfoil and look at the mesh structure.
5.2.2. Modify the Mesh plot settings¶
Double click on the Mesh plot to open the Mesh plot attributes window.
Experiment with settings for:
Mesh color
Opaque color
Opaque mode
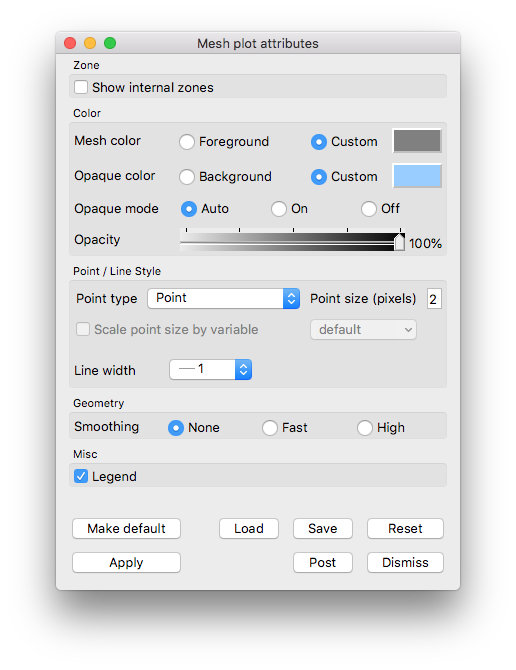
Fig. 5.39 Example mesh plot settings for the Potential Flow data.¶
You will need to click Apply to commit the settings to your plot.
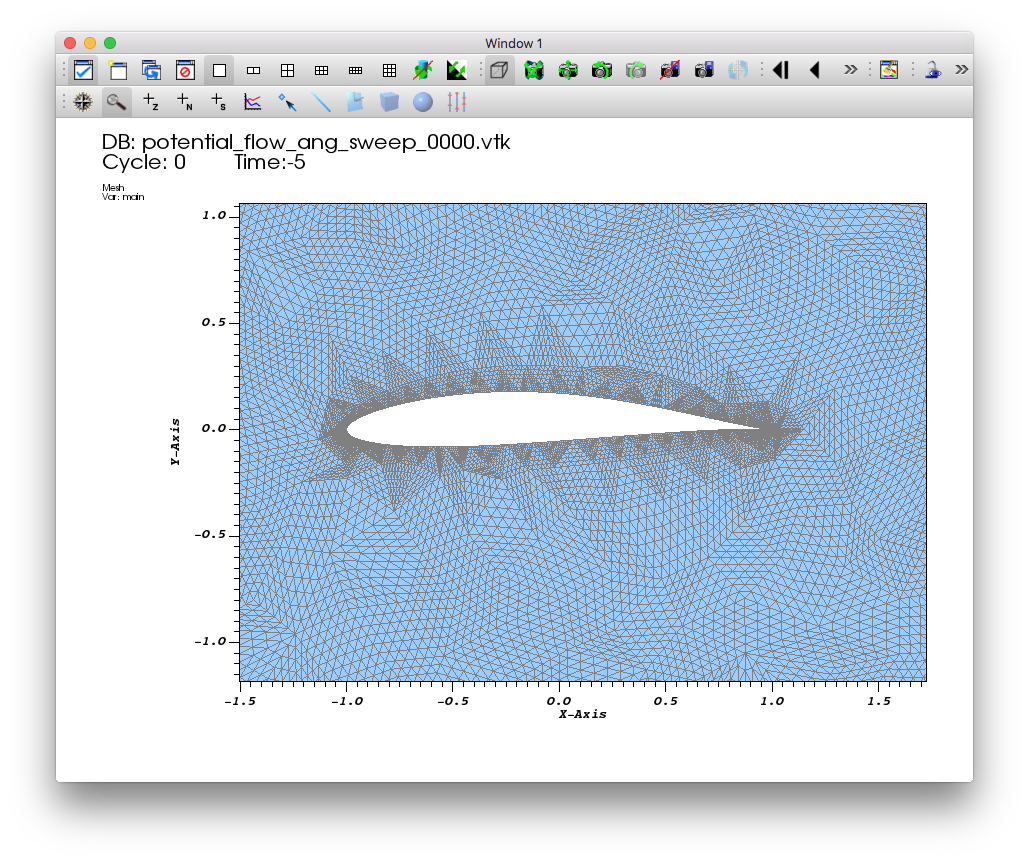
Fig. 5.40 Example mesh plot result the Potential Flow data.¶
5.3. Examining the velocity magnitude¶
In addition to the mesh topology, this dataset provides a vector field “v”, representing the velocity, associated with the mesh vertices.
VisIt automatically defines an expression that allows us to use the magnitude of the “v” vector field as a scalar field on the mesh. The result of the expression is a new field named “v_magnitude”.
We will use Pseudocolor plots to examine the “pressure” and “velocity_magnitude” fields.
Go to Add->Pseudocolor->v_magnitude.
Click Draw.
Double click on the Pseudocolor plot to bring up the Pseudocolor plot attributes window.
In the Limits section, enable the Maximum checkbox and set the limit to 1.
In the Color section,cChange the color table to Spectral and check the Invert button.
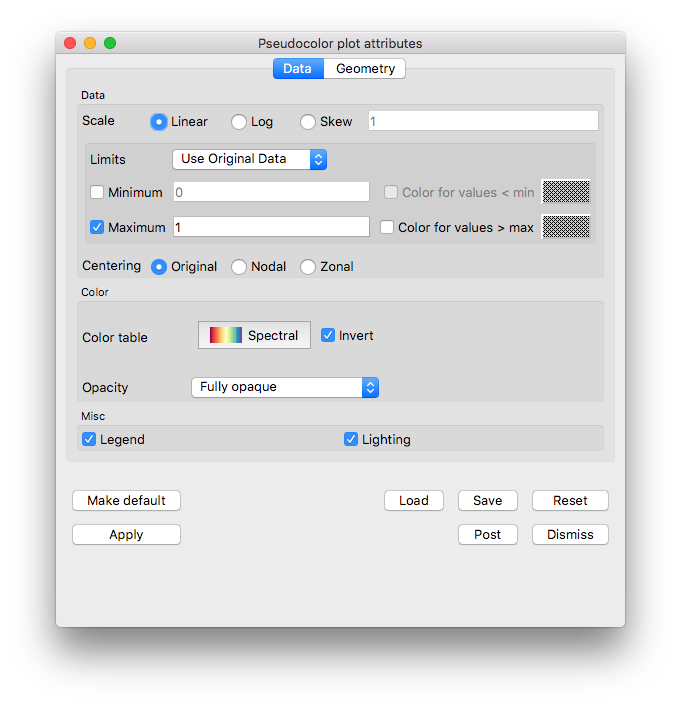
Fig. 5.41 The pseudocolor plot attributes for the velocity magnitude example.¶
Click Apply.
Click Draw.
Drag the Time animation controls above the plot list on the main GUI window.
You will see the velocity magnitude solutions for the different angles of attack.
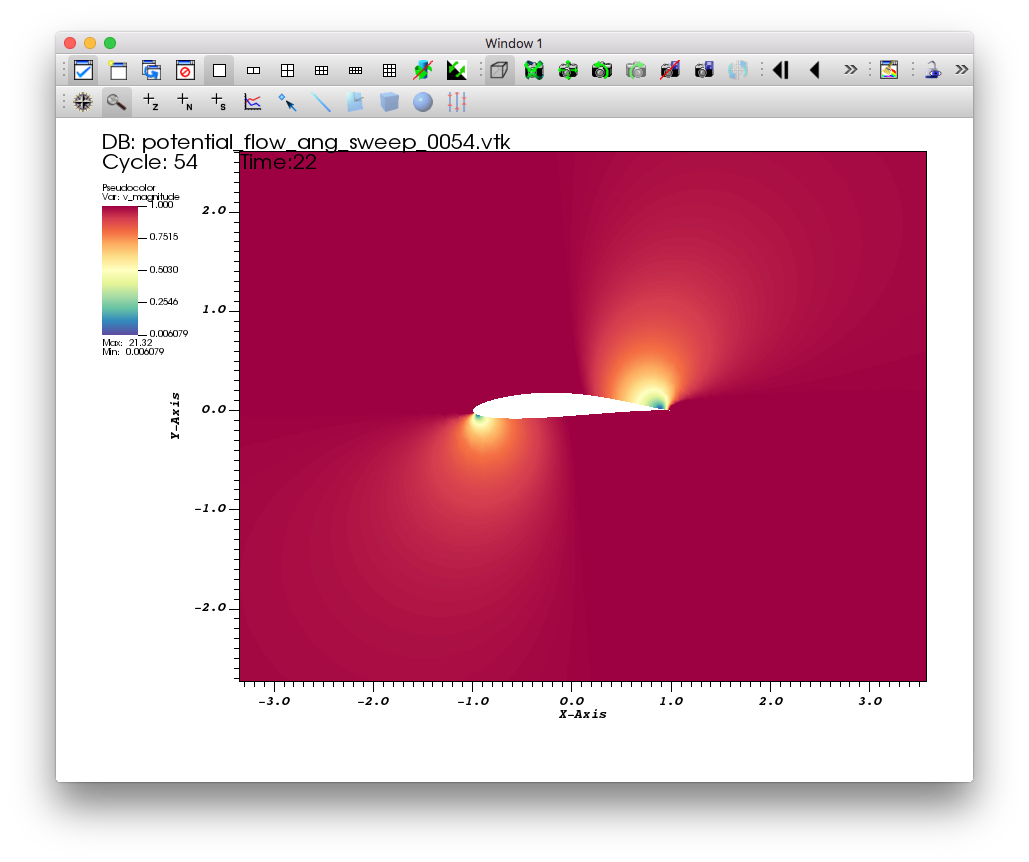
Fig. 5.42 The pseudocolor plot of the velocity magnitude.¶
Experiment with the Color for values > max option to see where the range is being clipped.
5.3.1. Contours of velocity magnitude¶
Now we will add an additional plot to view velocity magnitude contours
Go to Add->Contour->v_magnitude.
Double click on the Contour plot to bring up the Contour plot attributes window.
In the Contour Levels section, enable the Maximum checkbox and set the limit to 1.
In the Lines section, set the Line width to 2.
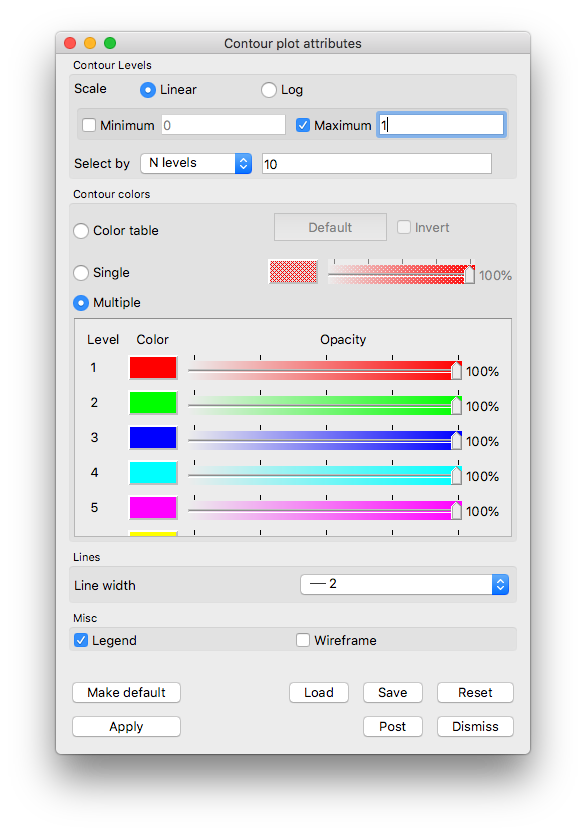
Fig. 5.43 Example contour plot settings for Potential Flow velocity magnitude.¶
Click Apply.
Click Draw.
Drag the Time animation controls above the plot list on the main GUI window.
You will see the contours of the velocity magnitude solutions for the different angles of attack.
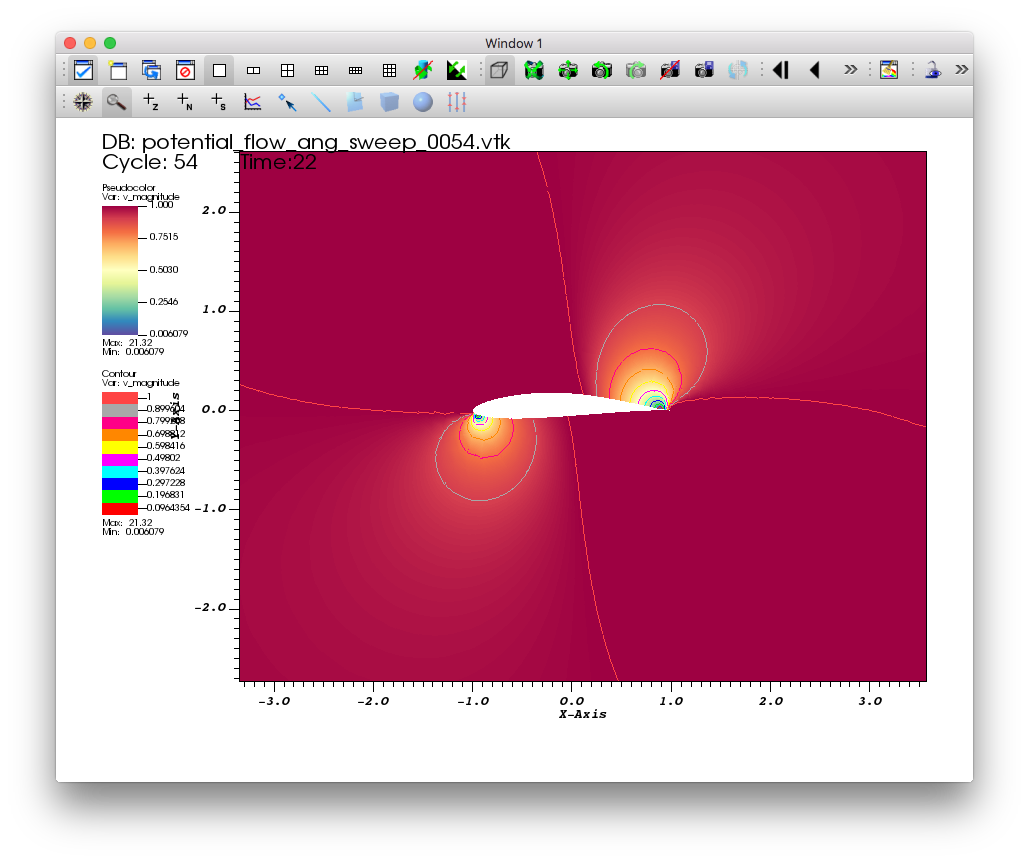
Fig. 5.44 A contour plot of the velocity magnitude.¶
Delete the contour plot when you are finished exploring, but keep the pseudocolor plot.
5.4. Visualizing the velocity vector field¶
This section of the tutorial outlines using glyphs and streamlines to visualize the velocity vector field from the simulation.
5.4.1. Plotting the vector field directly with glyphs¶
VisIt’s Vector plot renders a vector field at each time step as a collection of arrow glyphs. This allows us to see the direction of the vectors as well as their magnitude. We will create a vector plot to directly view the simulated “v” vector field.
Go to Add->Vector->v.
Open the Vector plot attributes window.
Go to the Vectors tab.
Set Stride to “17”.
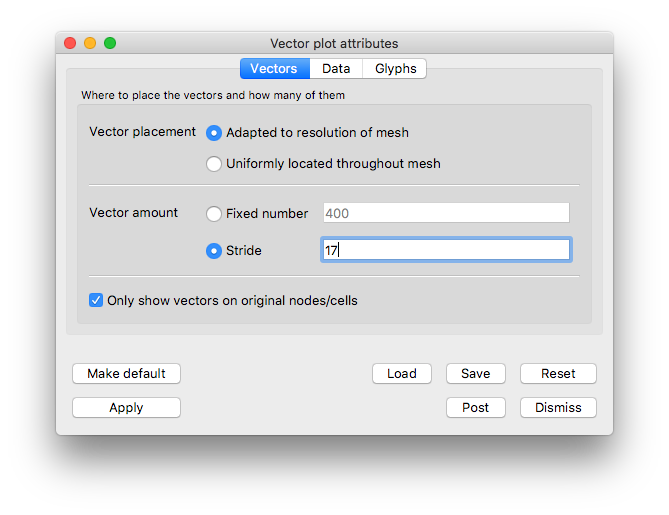
Fig. 5.45 Vectors tab settings for example vector plot of velocity¶
Go the the Data tab.
In the Limits section, enable the Maximum checkbox and set the value to “1”.
In the Color section, change the Magnitude to viridis
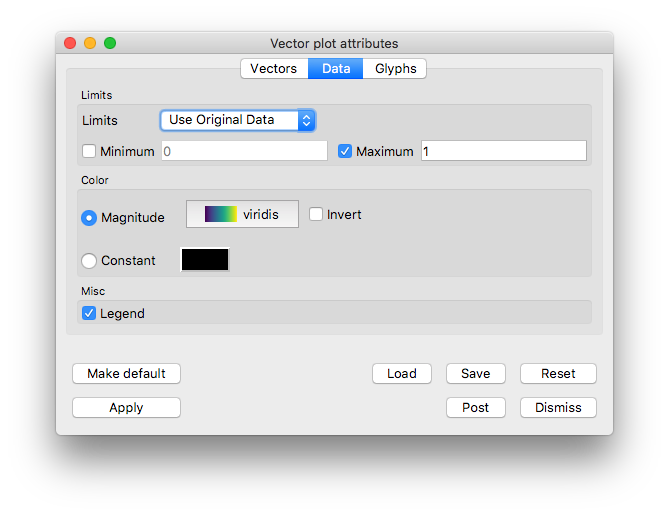
Fig. 5.46 Data tab settings for example vector plot of velocity¶
Go to the Glyphs tab.
In the Scale section, uncheck Scale by magnitude and Auto scale.
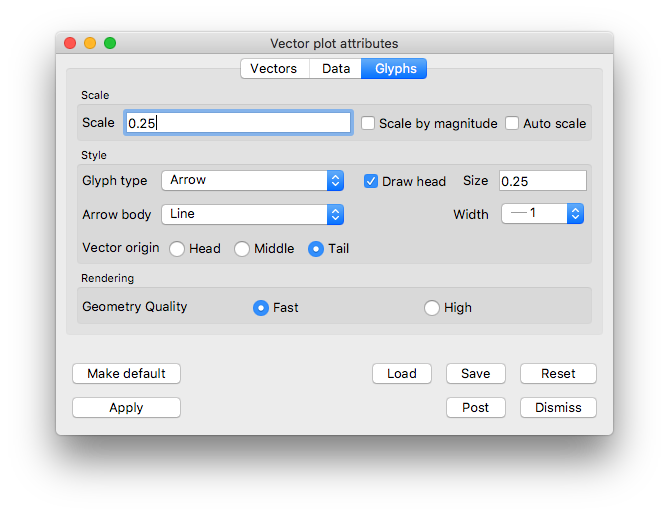
Fig. 5.47 Glyphs tab settings for example vector plot of velocity¶
Click Apply and Dismiss.
Click Draw.
Zoom in near the airfoil.
Drag the Time animation controls above the plot list on the main GUI window.
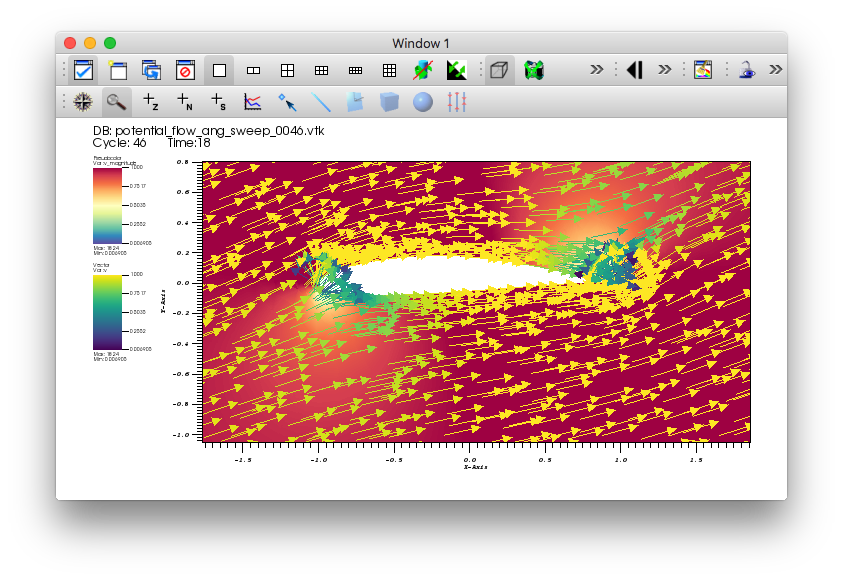
Fig. 5.48 The vector plot of velocity.¶
You will see glyphs of velocity solutions for the different angles of attack.
Delete the vector plot when you are finished exploring, but keep the pseudocolor plot.
5.4.2. Examining features of the flow field with streamlines¶
To explore the flow field further we will seed and advect a set of streamlines on the left side of the mesh. Streamlines show the path massless tracer particles would take if advected by a static vector field. To construct Streamlines, the first step is selecting a set of spatial locations that can serve as the initial seed points.
The flow moves left to right, we will use a vertical line of seed points on the left side of the mesh.
5.4.2.1. Plotting streamlines of velocity¶
Go to Add->Pseudocolor->operators->IntergralCurve->v.
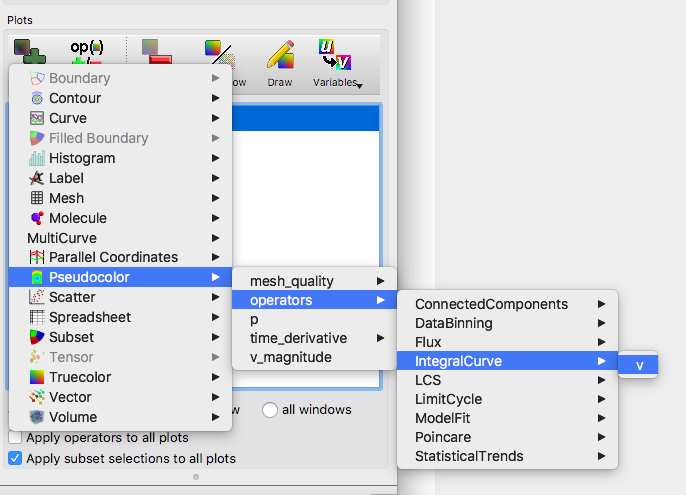
Fig. 5.49 Creating a streamline plot with the IntegralCurve operator.¶
Open the IntegralCurve operator attributes window.
Go to the Source section on the Integration tab.
Set the Source type to Line.
Set the Start to “-2 -2 0”, excluding any commas in the input text box.
Set the Stop to “-2 2 0”.
Set Samples along line to “10”.
Click Apply and Dismiss.
Click Draw on the Main GUI
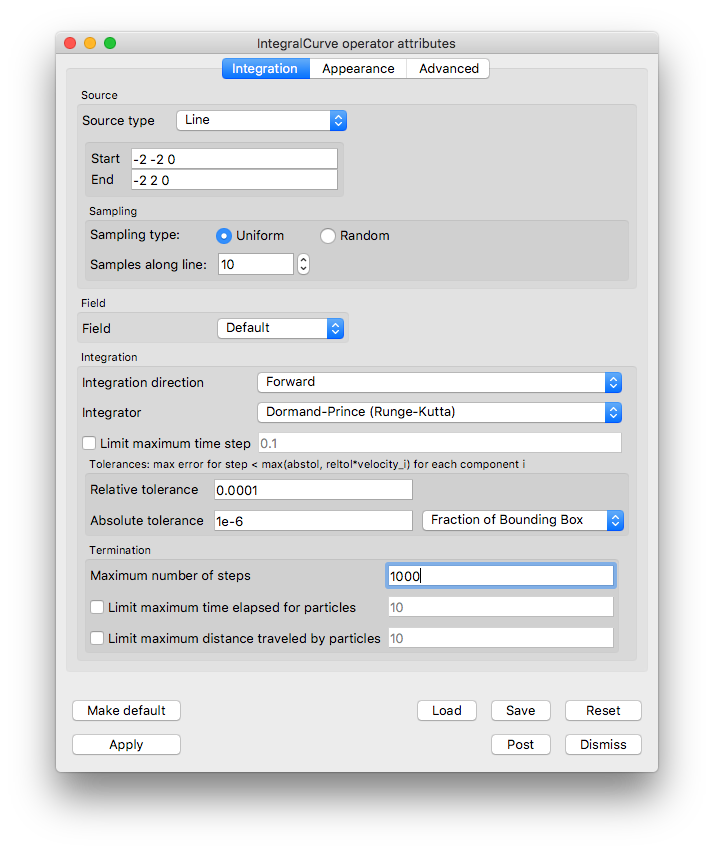
Fig. 5.50 The IntegralCurve operator attributes.¶
Open the Pseudocolor plot attributes window.
Go to the Data tab.
In the Color section set the Color table to viridis.
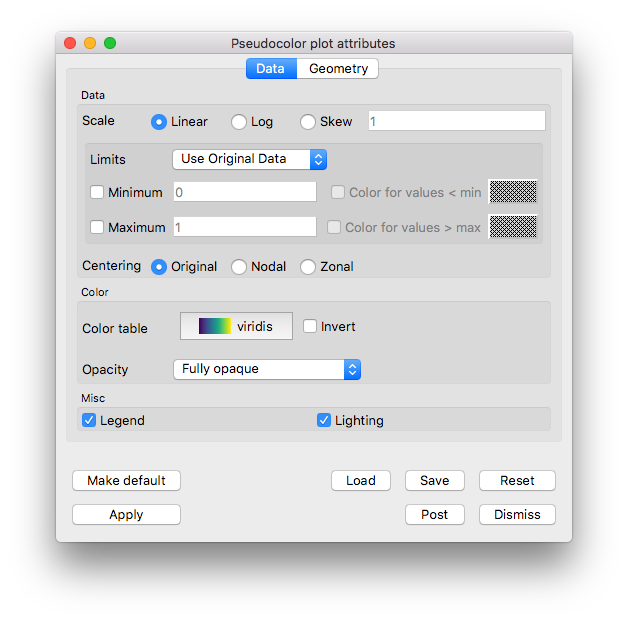
Fig. 5.51 The Pseudocolor attributes for the streamline data.¶
Go to the Line section on the Geometry tab.
Set Line type to Ribbons.
Set Tail to Sphere.
Set the tail Radius to “0.025”.
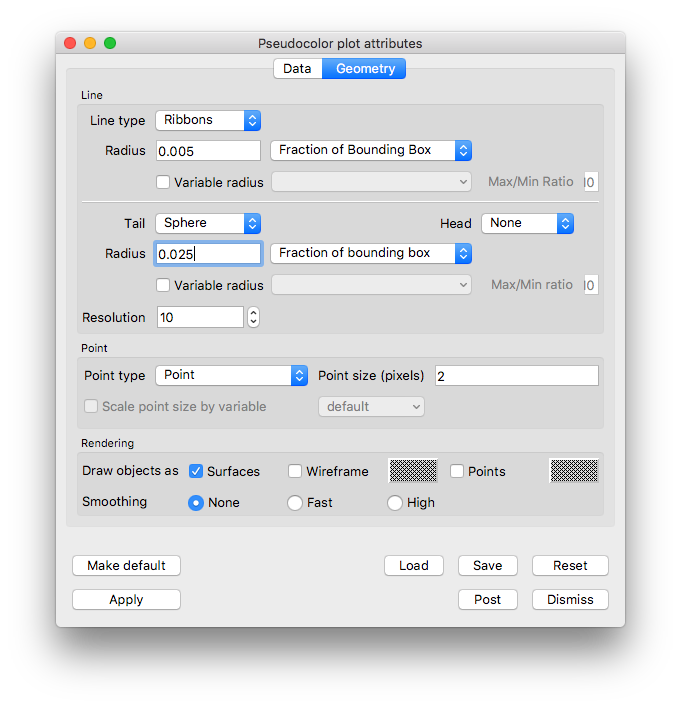
Fig. 5.52 The Pseudocolor attributes for the streamline geometry.¶
Click Apply and Dismiss.
Click Draw.
Use the time slider controls to view a few different angles of attack solutions.
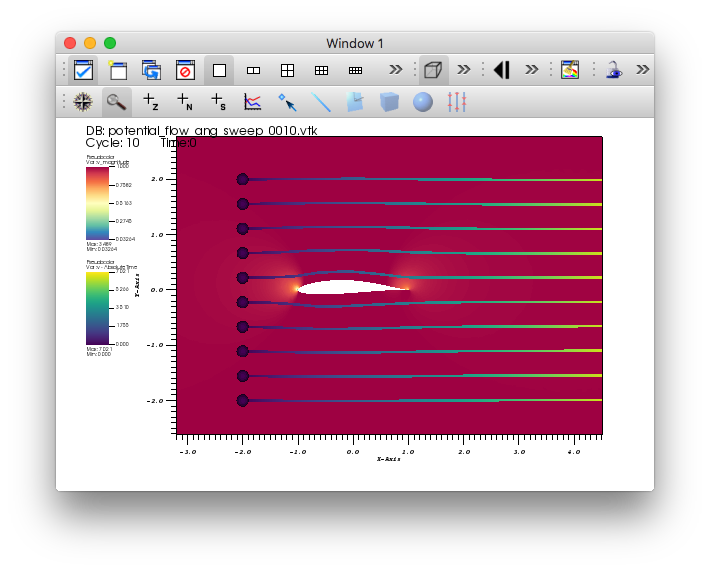
Fig. 5.53 The streamlines of velocity at 0 degree angle of attack.¶
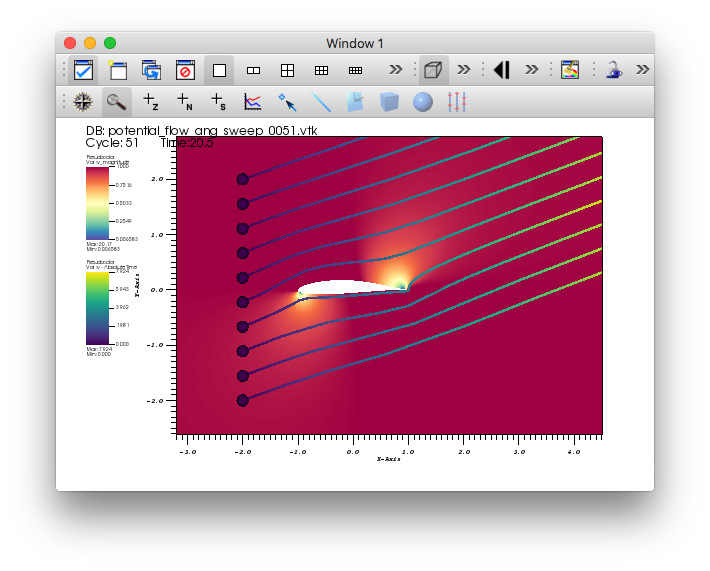
Fig. 5.54 The streamlines of velocity at 20.5 degree angle of attack.¶